はじめに

データ分析が必要な局面がぼちぼち出てきましたので、まずは簡単な決定木を用いて 分析結果の可視化をしようじゃないか、というのが今回の目論見です。

決定木とは

決定木とは、scikit-learnの1.8. Decision Treesによると、 分類や回帰を行うために使われる、ノンパラメトリックな教師あり学習のひとつ、とあります。 また、目的は、学習データ中の特徴(説明変数)を用いて、目的変数の推測を行えるモデルを作ること、だそうです。

ナンノコッチャ？ですので例を挙げますと、例えばある有料サービスに申し込んでくれる人を増やすために、 今までの履歴からどういったお客様が有料サービスに申し込んでくれたか、を調査するとします。 無料サービスA, B, Cがあったとして、どれとどれをどのくらい使っている人が 有料サービスを申し込んでくれるか、こういうことを考えたいわけですね。 ここで言う無料サービスA, B, Cが説明変数で、有料サービスに申し込むかどうかが目的変数になります。

決定木を使うことにより、Aのサービスを10回使って、かつCのサービスを1回以上使ったお客様は 有料サービスを申し込んでくれる可能性が高い、というモデルを構築することが出来ます。 また、モデルが構築できたら、そのモデルを用いて、有料サービスを申し込む前から 今までの行動から、お客様が有料サービスに申し込んでくれるかどうかを推定することができるようになるわけです。

必要なライブラリ

• Python (今回使うライブラリは2/3互換です。私は3.3系を使っています)
• scikit-learn (インストール方法はInstalling scikit-learn参照)
• pandas (インストール方法はInstallation参照)
• Graphviz (インストール方法はDownloadまたはMacならbrew install graphvizでOK)

分析の手順

データの準備

まずは自分の分析したいデータを用意します。…といっても、すぐに用意できないことがあるかと思いますので、 こちらに事前に調理しておいた…いやいや、日本語解説付きのデータセットがありますので、 気になるデータを使用してみてください。 統計を学びたい人へ贈る、統計解析に使えるデータセットまとめ

ここでは、Irisデータを使用します。

決定木の作成

データの読み込み・選定あたりでpandasを使用し、実際の学習でscikit-learnを使用します。 下記のようなコードを書き、実行してください。 graph.dotというファイルが生成されます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import pandas as pd
from sklearn import tree

# サンプルデータ(タブ区切り)の読み込み
data = pd.read_table('iris.txt')
# 説明変数
variables = ['Sepal.Length', 'Sepal.Width', 'Petal.Length', 'Petal.Width']

# 決定木の分類器を作成。各種設定は引数に与える
classifier = tree.DecisionTreeClassifier()
# 決定木の分類器にサンプルデータを食わせて学習。目的変数はSpecies
classifier = classifier.fit(data[variables], data['Species'])

# 学習した結果をGraphvizが認識できる形式にして出力する
with open('graph.dot', 'w') as f:
    f = tree.export_graphviz(classifier, out_file=f)

PDFによる可視化

上記のコードより得られる結果は graph.dot というファイルなのですが、 これだけ見てもよく分かりません。 そこで、下記コマンドを実行し、PDF変換します。

1

dot -Tpdf graph.dot -o graph.pdf

結果を見てみましょう。

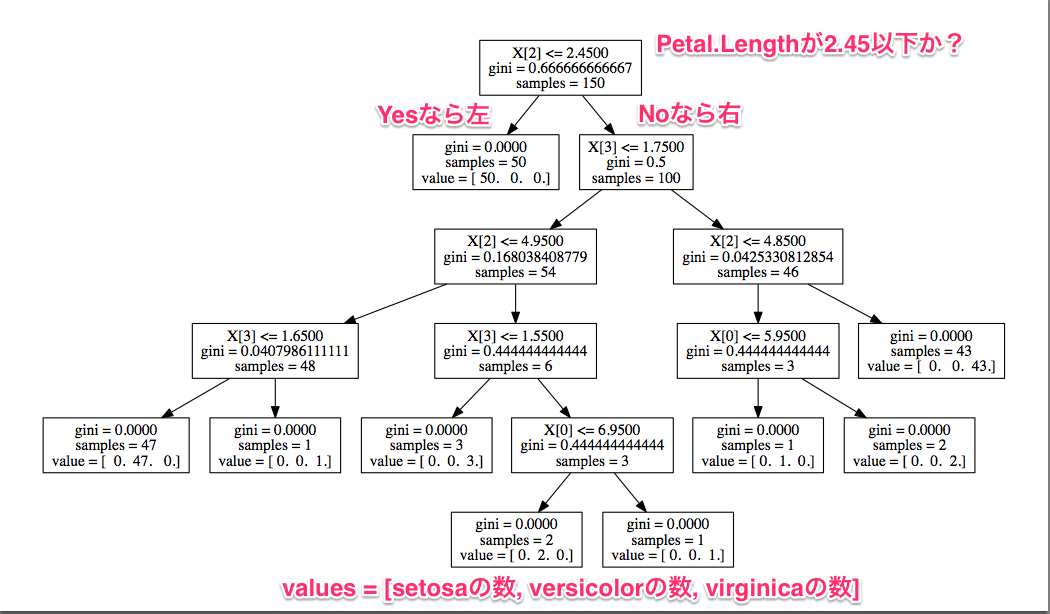
見方は、上から順番に、説明変数を0から数えて2番め(Petal.Length)が2.45以下か 否かで、Yesなら左、Noなら右に進んでいくことで分類していきます。 Yesならsetosa全データが入っているので、これは分類が容易だと分かります。 Noなら、次はPetal.Widthが1.75以下か否かで…というかたちで見ていけばよいです。

決定木は分類ルールが生成されるので、人にとっても解釈しやすいですね。

分類ルールは機能するのか？ ： 交差検定

ところで今回得られた結果には、大きな問題が2つあります。 ひとつは、未知のデータに対しても有効かどうかが分かりません。 もうひとつは、過学習している可能性が高いことです。

過学習とは、与えられた学習データにフィットしすぎた結果、 未知のデータに対して正しい分類ができない状態のことです。 今回の決定木も、非常に細かいところまで分類しています。 例えばPetal.Width <= 1.75のとき、90%の確率でversicolorになるはずなのですが、 その条件下でPetal.Width > 1.65のときはvirginicaである、と分類しています。 要するに、1.65 < Petal.Width <= 1.75のときはvirginicaである、という 細かい分類をしてしまうわけです。 この結果は確かに与えられた学習データに対してはうまくいきますが、 未知のデータに対しては、分類が細かすぎて誤分類してしまう可能性が高まります。

そこで、分類データを何個かに分割して、大部分を決定木の作成に使用し、 残る一部のデータを、その決定木の性能測定に使用します。 この操作を「交差検定 (Cross-validation)」と言います。

早速交差検定をやってみましょう。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

import pandas as pd
import numpy as np
from sklearn import tree, cross_validation

data = pd.read_table('iris.txt')

# データがSpecies順になっているので、シャッフルする
data = data.reindex(np.random.permutation(data.index))
variables = ['Sepal.Length', 'Sepal.Width', 'Petal.Length', 'Petal.Width']

classifier = tree.DecisionTreeClassifier()

# ここが差分。交差検定を5分割して、4つのデータセットと1つの検証データに分けて精度を計算
# それを5回実施した結果を返す
scores = cross_validation.cross_val_score(classifier, data[variables], data['Species'], cv=5)

print(scores.mean(), scores)

結果は下記のように出力されます(データセットを本プログラム起動時にシャッフルしているため、 結果は常に異なった値になります)。 この場合、94.67%の精度で分類ができていることになります。何となく良さげな精度？ですが、 100個のデータを与えたら、5〜6個は間違えるよ、という精度ですね。

1

0.946666666667 [ 1.          0.93333333  1.          0.9         0.9       ]

過学習の対策

決定木の過学習を抑える対策は、大きく分けて2つあります。

1. 子ノードに存在するデータ数の最小値を設ける
2. ツリーの深さを制限する

1.の方は、先ほどのPetal.Widthの例を防ぐ事ができるようになります。 本設定を使用するには、tree.DecisionTreeClassifierのコンストラクタ引数で設定を入れましょう。

1

classifier = tree.DecisionTreeClassifier(min_samples_leaf=2)  # 最低2件のデータが必要

2.の方の設定は、下記のように行います。 ルートノードを0として、子ノードまでが1、孫ノードまでが2…と設定します。

1

classifier = tree.DecisionTreeClassifier(max_depth=3)

そして、2つのパラメーターをどう設定するのが良いか…これはもう計算してもらいましょう。 min_samples_leafを1〜7、max_depthを2〜8、それぞれの組み合わせで精度を計算します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

import pandas as pd
import numpy as np
from sklearn import tree, cross_validation

data = pd.read_table('iris.txt')
data = data.reindex(np.random.permutation(data.index))
variables = ['Sepal.Length', 'Sepal.Width', 'Petal.Length', 'Petal.Width']

for min_samples_leaf in range(1, 7):
    for max_depth in range(2, 8):
        classifier = tree.DecisionTreeClassifier(
                min_samples_leaf=min_samples_leaf, max_depth=max_depth)
        scores = cross_validation.cross_val_score(classifier, data[variables], data['Species'], cv=5)
        print('{0:.3f}\t{1}\t{2}'.format(scores.mean(), min_samples_leaf, max_depth))

結果はこちら。平均精度、min_samples_leaf、max_depthの順番です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

0.933    1   2
0.953 1   3
0.947 1   4
0.953 1   5
0.953 1   6
0.940 1   7   # 未設定時
0.933 2   2
0.953 2   3
0.940 2   4
0.940 2   5
0.940 2   6
0.940 2   7
0.933 3   2
0.967 3   3   # 最良
0.967 3   4
0.967 3   5
0.967 3   6
0.967 3   7
0.933 4   2
0.960 4   3
0.960 4   4
0.960 4   5
0.960 4   6
0.960 4   7
0.933 5   2
0.960 5   3
0.960 5   4
0.960 5   5
0.960 5   6
0.960 5   7
0.933 6   2
0.947 6   3
0.947 6   4
0.947 6   5
0.947 6   6
0.947 6   7

100個のデータを与えたら6個間違えるパラメーター未設定時と比較し、最良の場合は 100個のデータを与えたら3〜4個間違える程度まで軽減されました。 ちなみにmin_samples_leaf=3, max_depth=3のときの決定木はこちら。

ちなみに、パラメーターの調整には、scikit-learnにGrid Searchなる機能があり、 各種パラメーターを入れ替えながら検証してくれる仕組みがあります。 今回は使いませんでしたが、次回試してみるつもりです。

まとめ

Python + pandas + scikit-learn で決定木を計算する方法をご紹介しました。 また、精度の計算に交差検定を使う方法と、決定木で過学習を抑えるための方法をご紹介しました。

実際のデータに対して試してみると、思わぬ発見が出てきて楽しいですよ。 是非お試しください。